题目大意

给定 $n \times m$ 的网格图，每个格子有一个高度 $h_{i, j}$。给一个格子的高度增加 $x$ 需要花费 $x$ 的代价。你要调整某些格子的高度，使得不存在高度单调不下降的，从起点到终点的路径。求需要花费的最小代价。

数据范围：$n, m \le 50$。

思路分析

看到 “不存在……的路径” 就想到最小割建图。但是直接对于每对相邻的格子建图不可行，因为一个格子高度的增加可能同时影响到与之相邻的几个格子。也就是说，如果需要使格子 $x$ 的高度比格子 $y_1, y_2, \cdots, y_k$ 大，所需要的代价不是 $\sum_{i = 1}^{k} \text{cost}(x, y_i)$，而是 $\max_{i = 1}^{k} \text{cost}(x, y_i)$，其中 $\text{cost}(x, y)$ 表示格子 $x$ 要比格子 $y$ 高需要花费的代价，也就是 $\max\{0, h(y) - h(x) + 1\}$。

所以，我们对于每个格子拆点，一起考虑它周围一圈的格子。例如对于下图中的格子：

图 1

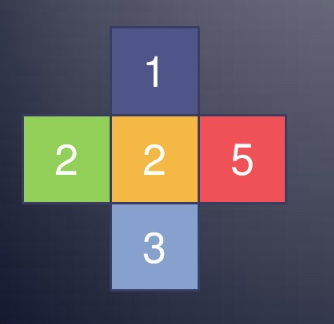
需要建如下结构的图：

图 2

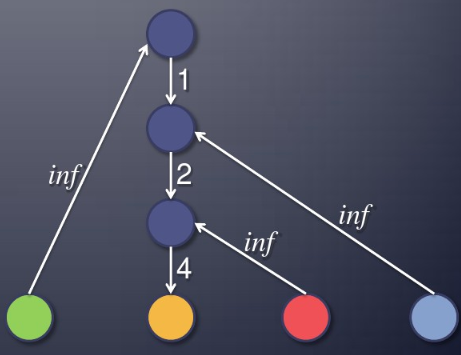
另外注意一些小细节：

$-1$ 最好提前判掉，否则可能会引起不必要的麻烦。
起点和终点的建图需要特判，因为题意要求起点和终点的高度不能变化。

代码实现

本菜鸡的 Dinic 跑不过（明明各种优化都加满了啊 QAQ），所以使用了 ISAP 来实现最大流。

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;

const int maxn = 12500, maxm = 4e4, inf = 1e9 + 1;
const int dx[] = { -1, 0, 1, 0 }, dy[] = { 0, 1, 0, -1 };
int T, n, m, Rr, Cr, Rt, Ct, s, t, mx, a[maxn + 3], b[5], c;
int tot, ter[maxm + 3], wei[maxm + 3], nxt[maxm + 3], lnk[maxn + 3], dep[maxn + 3], gap[maxn + 3], cur[maxn + 3];
queue<int> Q;

inline int id(const int &x, const int &y) {
	return (x - 1) * m + y;
}

inline int adj(int x) {
	return x & 1 ? x + 1 : x - 1;
}

bool check(int Rr, int Cr, int Rt, int Ct) {
	if (Rr == Rt && Cr == Ct) return true;
	if (abs(Rr - Rt) + abs(Cr - Ct) > 1) return false;
	return a[id(Rr, Cr)] >= a[id(Rt, Ct)];
}

bool comp(int x, int y) {
	return a[x] > a[y];
}

void add_edge(int u, int v, int w) {
	ter[++tot] = v, wei[tot] = w;
	nxt[tot] = lnk[u], lnk[u] = tot;
}

void add_fedge(int u, int v, int w) {
	add_edge(u, v, w), add_edge(v, u, 0);
}

void ibfs(int s, int t) {
	memset(gap, 0, sizeof(gap));
	memset(dep, 0, sizeof(dep));
	dep[s] = 1, Q.push(s);
	for (int u; !Q.empty(); ) {
		u = Q.front(), Q.pop();
		gap[dep[u]]++;
		for (int i = lnk[u], v, w; i; i = nxt[i]) {
			v = ter[i], w = wei[adj(i)];
			if (dep[v]) continue;
			dep[v] = dep[u] + 1, Q.push(v);
		}
	}
}

int dfs(int u, int flow, int s, int t) {
	if (u == t) return flow;
	int ans = 0;
	for (int i = cur[u], v, w, x; i && ans < flow; i = nxt[i]) {
		v = ter[i], w = wei[i];
		if (w && dep[v] == dep[u] - 1) {
			cur[u] = i, x = dfs(v, min(flow - ans, w), s, t);
			ans += x, wei[i] -= x, wei[adj(i)] += x;
		}
	}
	if (ans < flow) {
		if (!--gap[dep[u]]) dep[s] = mx + 1;
		++gap[++dep[u]], cur[u] = lnk[u];
	}
	return ans;
}

int flow(int s, int t) {
	ibfs(t, s);
	int ans = 0;
	memcpy(cur, lnk, sizeof(lnk));
	while (dep[s] <= mx) {
		ans += dfs(s, inf, s, t);
	}
	return ans;
}

int main() {
	scanf("%d", &T);
	while (T--) {
		scanf("%d %d", &n, &m);
		scanf("%d %d %d %d", &Rr, &Cr, &Rt, &Ct);
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				scanf("%d", &a[id(i, j)]);
			}
		}
		if (check(Rr, Cr, Rt, Ct)) {
			puts("-1");
			continue;
		}
		s = id(Rr, Cr), t = id(Rt, Ct), mx = id(n, m);
		tot = 0, memset(lnk, 0, sizeof(lnk));
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				if (id(i, j) == s || id(i, j) == t) {
					for (int k = 0, x, y; k < 4; k++) {
						x = i + dx[k], y = j + dy[k];
						if (x < 1 || x > n || y < 1 || y > m) continue;
						if (a[id(x, y)] >= a[id(i, j)]) {
							add_fedge(id(x, y), id(i, j), inf);
						} else {
							add_fedge(id(x, y), id(i, j), 0);
						}
					}
					continue;
				}
				c = 0;
				for (int k = 0, x, y; k < 4; k++) {
					x = i + dx[k], y = j + dy[k];
					if (x < 1 || x > n || y < 1 || y > m) continue;
					if (a[id(x, y)] >= a[id(i, j)]) b[++c] = id(x, y);
				}
				sort(b + 1, b + c + 1, comp);
				int tmp = id(i, j);
				for (int k = 1; k <= c; k++) {
					++mx, add_fedge(b[k], mx, inf);
					add_fedge(mx, tmp, a[b[k]] - a[id(i, j)] + 1), tmp = mx;
				}
			}
		}
		printf("%d\n", flow(s, t));
	}
	return 0;
}